We had already know that in electrostatics, Gauss's theorem, according to which, the surface integral of electrostatic field E‾ over a closed surface S is equal to 1/?0 times the total charge q inside the surface, where ?0 is absolute electrical permittivity of free space i.e.

If an electric dipole were enclosed by the surface, equal and opposite charges in the dipole add up to zero. Therefore, surface, integral of electric field of a dipole over a closed surface enclosing an electric dipole is zero i.e.

Whereas electric field can be produced by isolated charge, the magnetic field is produced only by a magnetic dipole. This is because isolated magnetic poles do not exist. Hence, magnetic analogue of eqn. (2) is

i.e. surface integral of magnetic field over a surface (closed or open) is always zero. i.e. the net magnetic flux ØB through any surface S is always zero. This is called Gauss's law in magnetism. In terms of magnetic field lines, the law means that there are as many lines entering S, as are leaving it.
Gauss's theorem in magnetism establishes that:
Isolated magnetic poles called monopoles do not exist, or
In magnetism, there is no counterpart of isolated free charge in electricity, or
Magnetic poles always exist in unlike pairs of equal strength.
Thus corresponding to eqn. (1) of Gauss's theorem in electrostatics, we can visualize eqn. (3) as
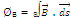
= µ0 /4∏ (m) + µ0 /4∏ (- m) = 0
Where m is strength of N-pole and - m is strength of S-pole of same magnet. µ0 is absolute magnetic permeability of free space.
ExpertsMind.com - Magnetism Gauss Law Assignment Help, Magnetism Gauss Law Homework Help, Magnetism Gauss Law Assignment Tutors, Magnetism Gauss Law Solutions, Magnetism Gauss Law Answers, Electromagnetism Assignment Tutor