mathematics - Determinants and Matrices, Math

Determinant: Consider the set of linear equations a₁x + b₁y = 0 and a₂x + b₂y = 0, where on eliminating x and y we get the eliminant a₁b₂ - a₂b₁ = 0; or symbolically, we write in the determinant 

 

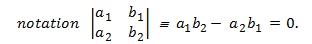
2×2 order having 2 rows and 2 columns. Similarly, a determinant of 3 × 3 order can be expanded as:

 

 

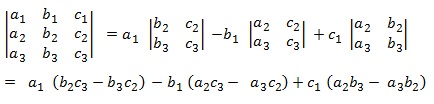
The sign is determined as positive or negative according as the permutation is even or odd. 

 

Properties of a Determinant: 

1. If all the elements of a row (column) are zero, then the value of the determinant is zero. 

2. If the rows (columns) of a determinant are changed into columns (rows) the value of the determinant remains unaltered. 

3. If the elements of a row (column) are identical proportional to the elements of any other row (column), then the determinant vanishes. 

4. The interchange of any two rows (columns) of a determinant changes its value in its sign only. 

5. If all the elements of a row (column) of a determinant are multiplied by a constant k, then the value of the determinant gets multiplied by k. 

6. If the elements of a row (column) of a determinant area expressed as the sum (difference) of two quantities, then the determinant can be expressed as the sum (difference) of two determinants of the same order.

Matrices: If a system of m linear equations in n unknowns is given as

a₁₁X₁ + a₁₂x₂ + ......... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ......... + a_2nx_n = b₂

................................................

a_m1xa + a_m2x₂ +.........+ a_mnx_n = b_m

 

Called an m × n .matrix with elements a1(i = 1, 2, ..... m; J = 1. 2.. n) over the field of real (complex) numbers. 

Types of Matrices 

Square matrix: A matrix in which the number of rows is equal to the number of columns is called a square matrix. 

Identity matrix: A square matrix A all of whose non-diagonal elements are zero (i.e., it is a diagonal matrix) and also all the diagonal elements are unity is called a unit matrix or an identity matrix. 

Zero matrix or Null matrix: Any m × n matrix in which all the elements are zero is called a zero matrix or null matrix of the type m × n and is denoted by Om×n.

Row matrix: A 1 × n matrix having only one row is called a row matrix. e.g., A = [a11 a12 ....... a1n]1xn. 

Column matrix: A n × 1 matrix having only one column is called a column matrix 

Matrices and Determinants Math Assignment Help - Homework Help at Expertsmind.com

Expertsmind.com offers math solutions for matrix, and determinants mathematics homework and assignments. At Expertsmind the expert tutors are helping students by providing help with your child's homework and assignments. Our experts are available for 24*7 hours for help, We provide our students with a proficient service of Math Homework and Assignment related help. You just need to send your Math Assignment or Math Homework at our desired E-mail ID I.e. [email protected] or upload it at our website. Once our highly competent math tutors analyze your assignment, we will get back with an appropriate price quote. Then you have to make the payment through any of the various means listed on the website home page. At Expertsminds, delivery of every piece of work on time is given utmost priority and treated as a responsibility.