Correlation and Regression
Univariate distributions: These are the distributions in which there is only one variable such as the heights of the students of a class.
Bivariate distribution: Distribution involving two discrete variable is called a bivariate distribution. For example, the heights and the weights of the students of a class in a school.
Bivariate frequency distribution: Let x and y be two variables. Suppose x takes the value x1, x2, ... , xn and y takes the value y1, y2, ... yn, then we record our observations ill the form of ordered pairs (xi, yi), where 1 ? j ? n, 1 ? j ? n. lf a certain pair occurs fij. times, we say that its frequency is fij.
The function which assigns the frequencies fij 's to the pairs (xj yj) is known as a bivariate frequency distribution.
Two way frequency tables: In such tables, the top row consists of the values of the variable x and the left hand column consists of the values of the y. The frequencies corresponding to a pair of values are written in the cell at the intersection of the relevant row and column.
The column total provide the univariate frequency distribution of x and the row totals provide the univariate frequency distribution of y. These column totals and the row totals are know as the marginal frequency distribution of x and y respectively,
Conditional frequency distribution: For some fixed values of x the frequencies with which the various y values occur, when listed give the conditional distribution of y on x.
Similarly for some fixed values of y, the frequencies with which various x values occur, when listed give the conditional frequency distribution of x on y.
Correlation: The relationship between two variables such that a change in one variable results in a positive or negative change in the other variable is known as correlation.
Types of Correlation:
(i) Perfect correlation: If the two variable vary in such a manner that their ratio is always constant, then the correlation is said to be perfect.
(ii) Positive or direct correlation:
If an increase or decrease in one variable corresponds to an increase or decrease in the other, the correlation is said to be positive.
(iii) Negative or indirect correlation: If an increase or decrease in one variable corresponds to a decrease or increase in the other, the correlation is said to be negative.
Co-variance: The co-variance between two variables x and y takes the x1, x2, x3 ........ xn and y1, y2, y3, ….... yn is defined as
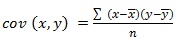
cov (x,y) = (∑¦? (x-¯x)(y-¯y) ?)/n
Where ¯x and ¯y are the means of x and y series respectively.
Coefficient of Correlation: Karl Pearson gave the following formula for the calculation of correlation coefficient
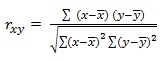
r_xy= (∑¦? (x-¯x) (y-¯y) ?)/√(∑¦(x-¯x) ^2 ∑¦(y-¯y)^2 )
Where x, v, ¯x and ¯y have usual meanings.
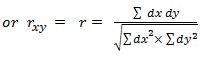
or r_xy = r= (∑¦? dx dy?)/√(∑¦dx^2× ∑¦?dy^2 ?)
where dx = (x - ¯x), dx2 = (x – ¯x)2
dy = (y-¯y) and dy2 = (y-¯y)2.
Modified formula:
r = 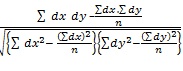
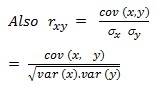
Rank correlation:
p=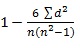
Where ∑¦d^2 = sum of the squares of the difference of two ranks and n is the number of pairs of observations.
Regression Analysis: In a statistical relationship, if the value of one variable is known, we can estimate the value of the another variable through a procedure known 'as regression analysis,
Regression Line of y on x: If value of x is known, then the value of y can be found as
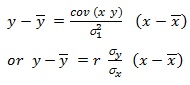
Regression Line of x on y: It estimates x for the given value of y as
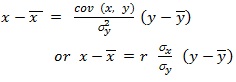
Regression Coefficients:
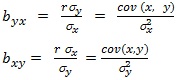
Important Points about Correlation Coefficient (r):
(1) r lies between - 1 and + 1
(2) The correlation is
(i) Perfect and positive if r = + 1
(ii) Perfect and negative if r = - 1
(iii) Not correlated if r = 0
(iv) Positive if r > 0
(v) Negative if r < 0
(3) It is independent of the change of origin and scale,
(4) It is a pure number and hence unitless.
(5) If x and yare independent, then r = 0
Important Points about Regression Coefficients bxy and byx:
(1) r=√(byx.bxy ) i.e., the coefficient of correlation is the geometric mean of the coefficients of regression.
(2) If bxy > 1, then bxy < 1 i.e., if one of the regression coefficient is greater than unity, then the other will be less than unity.
(3) If the correlation between the variables is not perfect, then the regression lines intersect at (x, y).
(4) byx is called the slope of regression line y on x and bXY is called the slope of regression line x on y.
(5) byx + bxy > 2 √(byx.bxy ) or byx + bxy > 2r i.e., the arithmetic mean of the regression coefficient is greater than the correlation coeffident.
(6) Regression coefficients are independent of change of origin but not of scale. -
(7) The product of lines of regression's gradients is given by
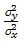
(8) If the angle between lines of regression is a, then tan ? =

(9) If both the lines of regression coincide, then correlation will be perfect linear.
(10) If both byx and bxy are positive, there will be positive and if both byx and bxy are negative, then r will be negative.
Important Points on Regression Lines:
(1) If r = 0, then tan a is not defined i.e., ∅ = Π/2. Thus the regression lines are perpendicular.
(2) If r = + 1 or - 1, then tan ∅ = 0 i.e., ∅ = 0.
Thus the regression lines are coincident.
(3) If regression lines are y = ax + b and
x = cy + d, then ¯x = (bc+d)/(1-ac) and ¯y=(ad+c)/(1-ac).
Standard Error of Prediction: The deviation of the predicted value from the observed value is known as the standard error of prediction and is defined as
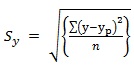
Where y is actual value and yp is predicted value.
In relation to coefficient of correlation, it is given by
(i) Standard error of estimate' of x is
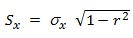
(ii) Standard error of estimate of y is

Live Math Experts: Help with Correlation and Regression Assignments - Homework
Expertsmind.com offers help with Correlation and Regression assignment and homework in mathematics subject. Experts mind’s math experts are highly qualified and experienced and they can solve your complex Correlation and Regression math problems within quick time. We offer email based assignment help –homework help service in all math topics including Correlation and Regression .
Math Online Tutoring: Correlation and Regression
We at Expertsmind.com arrange instant online tutoring session in Correlation and Regression math topic. We provide latest technology based whiteboard where you can take session just like live classrooms. Math experts at expertsmind.com make clear concepts and theory in Correlation and Regression Math topic and provide you tricky approach to solve complex Correlation and Regression problems.