Phasor Diagram of an Induction Motor:
Induction motor is analogous to the transformer. For the stator winding
V1 =- E1 + I1 (R1 + j X1 )
where V1 = Supply voltage per phase,
I1 = Stator current per phase,
R1 = Stator resistance per phase,
X1 = Stator leakage reactance per phase, and
E1 = Voltage induced per phase in the stator.
and also,
E1 = 4.44 φ f N1 kw1
Where φ = Mutual flux per pole,
f = Stator frequency,
N1 = Stator winding turns per phase, and
kw1 = Winding factor of stator.
We know that rotor winding is short circuited at the ends
V2 = 0 = E2 s - I2 ( R2 + j X 2 s )
where I2 = Rotor current per phase,
R2 = Rotor resistance per phase, and
X2s = Leakage reactance of rotor at slip frequency per phase.
X 2s = 2π f2 L2 ;
f2 = S f
X 2 s = 2π S f2 L2
X 2 s = S X 2
where X2 = Leakage reactance of rotor as stand fill per phase, and
E2s = Induced emf per phase in the rotor of induction motor.
E2 s = 4.44 φ f2 N2 Kw2
= S E2
where E2 = Induced emf in rotor per phase at stand still,
N2 = Rotor winding turns per phase, and
Kw2 = Winding factor of rotor.
From the Eqs. (39) and (41), we have
E1/ E2 = N1 Kw1 /N2 Kw2 = N1′ / N2′ = a
where, N1′ and N2′ are the effective number of stator and rotor turns respectively and "a" is called the effective turns ratio of an induction motor.
| V1 | ≈ | E1 |
Since the value of R1 and X1 are small.
The exciting current in the induction motor is specified by
I¯0 = I¯i + ¯Im
Where Im is the per phase value of the magnetising component of the exciting current and I¯i is the per phase value of the loss component of the exciting current.
The no load current in induction motor is more than that of transformer due to the air gap among the stator and rotor winding.
From the current and voltage equations discussed above, we may develop the phasor diagram.
The rotor power factor angle at any slip, S is
θ = tan -1 (S X 2 / R2
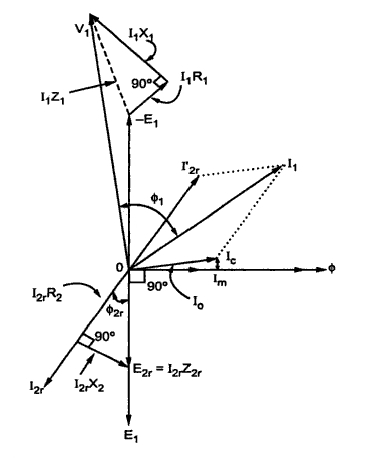
Figure: Phasor Diagram of an Induction Motor for a > 1 and S < 1
where
I2′ = (N2' /N1′ )I2 = (1/a) I2
and
I¯1 = I¯0 + I¯2′