Supply and Demand Curves
In microeconomics, the term supply refers fairly factually to the amount or amount of a product obtainable for expenditure in a given market. The term insist, however, is a measure of how much a customer wants a product, spoken as a function of how much that consumer is eager to pay for the manufactured goods.
Supply and insist curves are explicit representations of each purpose in family member to the other. More simply put, a supply curve expresses the behavior of the sup- ply function, where measure serves as the independent or X axis, and price serve as the dependent or Y axis. Across these axes, the provide curve is a growing function. This represent the desire of firms to sell more (and thereby make greater quantities of product available) when price are high than when prices are low.
The command curves also express the performance of the command function across the same axes. This behavior, how- ever, is conflicting in nature, as demand is represent by a decreasing function. This means that when there is a lesser amount of a product available, people are willing to pay more for it. When manufactured goods are available in plentiful supply, community will pay less for it.
The point of crossroads of these two curves represents the price and measure amounts when a given market is in symmetry, or when supply equals demand. From this point, a manager can appraise the outcomes of changes in supply and the matching belongings on price, and vice versa for a meticulous product.
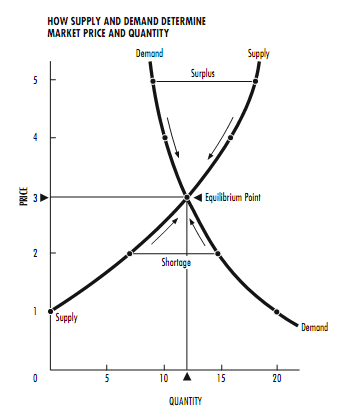
Fig : Supply Demand Curve
Managers can also use microeconomic tools to review the most and least principles for revenue, cost, and profit equations. To recognize these relationships, however, one must recognize what mechanism makes up these three equations.
Revenue, simply put, is all the money a firm makes before any operating cost are taken out. In other words, proceeds are equal to the number of units of product sold, times the price each unit is selling for. In its simplest form:
Revenue = price*quantity sold
Clearly, this equation increases in difficulty for firms that produce more than one product, but the general principle leftovers the same.
Cost equations are to some extent less uncomplicated than their proceeds counterparts. Total cost equations consist of variable costs, or costs that change depending on how many units a solid produces, and fixed costs, which do not change with production. An example of a variable cost would be material operating expenditure, while an example of a fixed cost would be a company's rent. Thus, in its easy form:
Total cost = variable cost * quantity sold + fixed costs
Profit equations calculate what a firm makes after it covers its expenses of production. This translates to a firm's revenues less its costs, or:
Profit = (price* quantity sold) - [(variable costs *quantity sold) + fixed costs]
For example, understand a New York City hot dog position paid $20 each day to rent the utensils and space on the avenue. If the situate charges the customer $5 for each hot dog and pays $3 for the raw equipment (uncooked hot dogs and buns) concerned in produce each hot dog, then the hot dog situate must sell 10 hot dogs to manage
0 = ($5 *10) - [($3 * 10) + 20]
0 = $50 - [30 + 20]
0 = $50 - $50
If the hot dog situate sells more than 10 hot dogs, the incremental earnings on each supplementary hot dog sold will be $2, as the fixed costs have been enclosed ($5 - $3 = $2). Otherwise, the price of the hot dogs could be raise to augment earnings. If the price goes up, however, the position may sell smaller amount hot dogs, as people opt for the $3 hot sausage avail- able down the street. Thus, as the price of hot dogs in- creases, the demand will decrease. This helps us to our next thought.