Torsional equation:

Derive the Torsional equation T/J = Π  /R = Gθ/L

Or

Derive an expression for the shear stress in shaft subjected to a torque.

Sol.: Assume,

T  = Maximum twisting torque or twisting moment

D = Diameter of shaft

R = Radius of shaft

J  = Polar moment of Inertia

τ= Maximum Permissible Shear stress (Fixed for given material)

G = Modulus of rigidity

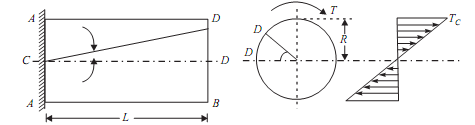
θ= Angle of twist (Radians) = angle D'OD L  = Length of shaft.

?= Angle D'CD = Angle of Shear strain

Than Torsion equation is: T/J =   τ/R = G. θ /L

Let the shaft is subjected to a torque or twisting moment 'T'. And hence every C.S. of this shaft will be subjected to shear stress.

Now distortion at the outer surface = DD'

Shear strain at outer surface = Distortion/Unit length tan?         = DD'/CD

i.e. shear stress at the outer surface (tan? ) = DD'/L or  = DD'/L           ...(i)

Now DD' = R.θ              or      ?= R .  θ /L    ...(ii)

Now G = Shar stress induced/shear strain produced

G =   τ/(R. θ /L);

or;                                             τ/R = G. θ /L                              ...(A);

This equation is called Stiffness equation.

Hear G,  θ , L are constant for a given torque 'T'. That is proportional to R

If τ r  be the intensity of shear stress at any layer at a distance 'r' from canter of the shaft, then;

Now from equation (ii) T = ( τ/R)   J

or                                              τ/R = T/J;                                   ...(B)

This equation is called as strength equation

The combined equation A and B; we get

T/J =   τ/R = G.  τ/L

This equation is called as Torsion equation.

From the relation             T/J =   τ/R ; We have  T =   τ.J/R =  τ .ZP

For the given shaft I_P  and R are constants and IP/R is thus constant and is called as POLAR MODULUS(Z_P). of the shaft section.

Polar modulus of section is thus measure of strength of shaft in the torsion.

TORSIONAL RIGIDITY or Torsional Stiffness (K): = G.J/L = T/θ