Reference no: EM13342651

PROBLEM 1: Distribution Management

Suppose that you are the distribution manager for a company. Currently, you need to plan the shipments of a product to three stores.

- Store 1 requires 50 units of the product each day
- Store 2 requires 40 units of the product each day
- Store 3 requires 70 units of the product each day

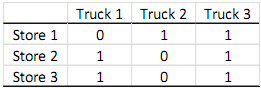
You have three trucks that you can use to make shipments to the stores. Each truck has a capacity of carrying 75 units of the product per day. Furthermore, each truck follows the same route every day. The table below shows whether a truck's route passes through a store or not (a value of 1 implies that truck passes through that store, and a value of 0 implies that the truck does not pass through that store).

That is, truck 1 can stop at Stores 2 and 3; truck 2 can stop at Store 1; and truck 3 can stop at Stores 1, 2, and 3 (the order of the stops to the stores on a truck's route is not important as the units can be loaded to the trucks accordingly). As the distribution manager, you want to determine how to load each truck by deciding on how many units of the product will be delivered to each by each truck. While doing so, you need to make sure that each store is delivered with exactly the number of units of the product they require. Furthermore, due to unloading operations, a truck cannot deliver more than 50 units per day to the same store. For instance, if truck 1 is loaded with 60 units, it cannot delivery all 60 units to store 3.

As the distribution manager, you want to make the shipment plan to minimize the total daily cost. Total daily cost is equal to the sum of the truck costs. Due to different total distances of the truck routes, truck 1 costs $10 per unit loaded, truck 2 costs $9 per unit loaded, and truck 3 costs $11 per unit loaded.

(Assume that you can ship fractional number of units to any store with any truck.)

a) Mathematically formulate a linear programming model for the above distribution management problem. Define your decision variables and the notation you use for them, express the objective and objective function, and constraints using your decision variables.

Combine everything to get the final linear model.

b) Mathematically formulate the following constraints:

a. The number of units delivered to Store 1 with truck 3 should be greater than or equal to the number of units delivered to Store 1 with truck 2.

b. Truck 3 should carry more than 40% of the total units carried by trucks 1 and 2.

c. You cannot deliver to Store 3 with truck 1.

c) Now suppose that you want to minimize the total weekly cost. Would the optimum solution of the model you formulated in part a change? Explain your reasoning briefly without solving the model in part a and the model with the weekly cost minimization.

PROBLEM 2 : Dr. Konur selling Iphone 6 and Iphone 6+ Dr. Konur decided to sell new Iphones in Rolla. Particularly, he will sell Iphone 6 (i6) and Iphone 6+ (i6+).

Due to regulations, Dr. Konur can sell at most 50 Iphones in total per week and he wants to sell at least 25 Iphones in total per week. In a week, he should not sell more i6+ than i6 and he should not sell more than 25 i6's. From each i6, he makes a $50 profit; and, from each i6+, he makes a $50 profit. Dr. Konur wants to maximize his total weekly profit from iphone sales by determining how many Iphone 6 and Iphone 6+ to sell each week.

a) Mathematically formulate a linear programming model for Dr. Konur's Iphone sales problem. Define your decision variables and the notation you use for them, express the objective and objective function, and constraints using your decision variables. Combine everything to get the final linear model.

b) Solve Dr. Konur's problem using graphical method. Draw the axes, constraints, and determine the feasible region and the corner points. Then, find the optimum solution or optimum solutions. Does the model have infeasibility, unique optimum, alternative optima, or unboundedness?

c) Now suppose that Dr. Konur is allowed to sell more than 25 i6s per week. How does the feasible region change? Does the model have infeasibility, unique optimum, alternative optima, or unboundedness now? Explain briefly.

d) Now, addition to be allowed to sell more than 25 i6s per week, suppose that Dr. Konur can sell as many Iphones as he wants per week. How does the feasible region change?

Does the model have infeasibility, unique optimum, alternative optima, or unboundedness now? Explain briefly.

PROBLEM 3: Manufacturing Planning

Suppose that you are the production manager of a product that your company manufactures. Particularly, a sub-product comes to your manufacturing department's buffer area initially. After that, this sub-product should go through two processes to become an end-product. First, it should go through process 1, and then it should go through process 2. There are different machines that can complete each process and each process can be completed by one machine.

- Process 1 (initial assembly) can be completed by machine A or machine B. Machine A can complete process 1 in 38 seconds. Machine B can complete process 1 in 34 seconds.

- Process 2 (final assembly) can be completed by machine C or machine D. Machine C can complete process 2 in 27 seconds. Machine D can complete process 2 in 24 seconds.

A sub-product in the buffer area, therefore, first should go to either machine A or machine B. The table below shows the time (in seconds) it takes a sub-product to be transferred to machine A or machine B from the buffer area.

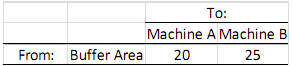
After process 1 is completed by machine A or machine B, the processed sub-product should go to either machine C or machine D for process 2. The table below shows the times (in seconds) it takes a sub-product to be transferred from machines A and B to machines C and D.

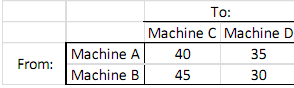
Finally, after process 2 is completed by machine C or D, the end-product should go to the inventory area. The table below shows the time (in seconds) it takes the end-product to be transferred from machines C and D to the inventory area.

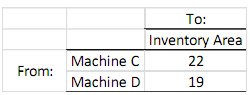
As the production manager, you want to determine the manufacturing plan for the sub-product so that you can minimize the total time it takes a sub-product to go from the buffer area to the inventory area as an end-product.

In this problem, you are asked to formulate the above production planning problem as a network optimization problem.

a) Represent the above production planning problem on a network and state it as a network optimization problem (i.e., min-cost flow, shortest path, or max-flow). To do so:
- Define the nodes, what they represent, and node values if any.
- Define the arcs, arc costs, arc capacities if any.
- The network you defined should not have node capacities, node costs, and undirected arcs.
- State the problem as a network optimization problem using the network.

b) Mathematically formulate the above network optimization problem as a min-cost flow or max-flow problem (if you stated the problem as a shortest path problem, recall that shortest path problems can be formulated as min-cost flow problems). Define your decision variables clearly and the notation you use for your decision variables, write the objective and objective function, and constraints. Combine everything to get the final model (you should not have any constraints other than flow-balance, arc-capacity, and non-negativity constraints).

PROBLEM 4: Sending Water through the Pipe Network

Suppose that you are the most famous fire fighter in Rolla, MO. Right now, there is a fire in one of the districts of Rolla. As the famous fire fighter, you want to stop this fire as fast as possible. To do so, you want to transfer as much water as possible from the water depot in Rolla to the district with fire using the pipe network in Rolla. Particularly, the pipe network is given below.

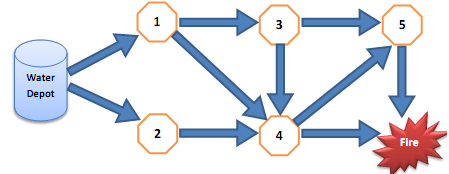
The water can be transferred from the water depot to city valves (there are 5 valves shown in orange octagons) and from some of the valves to the fire district. The table below shows how much water can be transferred in the pipes connecting the valves, water depot, and fire (the water can only flow in the direction of the pipes as given in the above network).

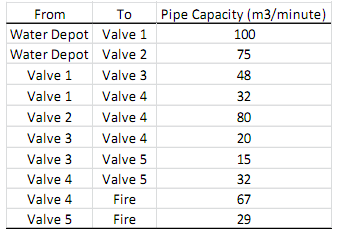
a) Mathematically formulate a network optimization problem for transferring as much water as possible from the water depot to the fire district. Assume that the water depot is sufficiently large and it has unlimited water in it. That is, mathematically formulate the above network optimization problem as a min-cost flow or max-flow problem (recall that shortest path problems can be formulated as min-cost flow problems). Define your decision variables clearly and the notation you use for your decision variables, write the objective and objective function, and constraints. Combine everything to get the final model.

b) Now suppose that the water depot has a capacity of 150 m3/minute. How would you modify the above network and your model in part a so that you still only have flow balance and arc capacity constraints. Formulate the additional constraints (you do not need to formulate the whole problem from start).